

The typical orientation for the three axes are shown below. The standard form of a two-variable linear equation is ax +by +c 0 a x + b y + c 0 where x x and y y are the two variables. The 3-D coordinate system has three perpendicular axes and uses ordered triples ( x, y, z) to represent a point in space. For example, 3x + 2y 8 is a linear equation in two variables. We will see each one, with examples in 2 variables, and in 3 variables. Solving Equations With Two Variables Linear Equation In Two Variables. So a System of Equations could have many equations and many variables. Let's take a quick look at how graphing is accomplished in 3-D: A System of Equations is when we have two or more linear equations working together. And like the "strange" situations we encountered in 2-D, there will also be the possibility of "strange" situations occurring in 3-D space. Most graphing calculators do not graph in 3-D. This poses a problem in that graphing in 3-D can be difficult to visualize since we are looking for the intersection of three planes (not three lines). When working with a 3x3 system where the three variables are each of degree one (such as x, y, and z), we are dealing with the 3-dimensional Cartesian space. There is also the possibility that we may be dealing with "strange" situations such as the lines being parallel (no solution), or the lines coinciding (lying on top of one another with an infinite number of solutions). Plug in this value in the other equation to. Such graphing may be done by hand or on a graphing calculator. Substitution method is the technique of rearranging either of the equations and making one variable the subject.
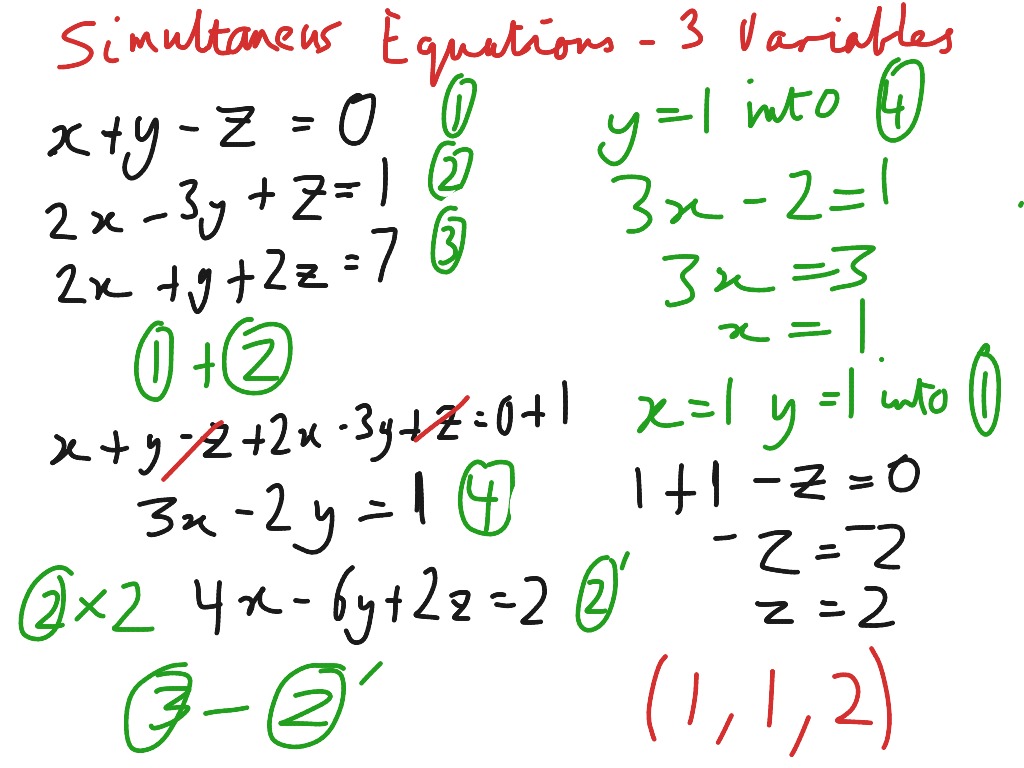
We can solve such a system by graphing the lines on a set of axes in the 2-dimensional Cartesian plane and finding the point of intersection. When working with a 2x2 system, for example, where the two variables are each of degree one (such as x and y), we are dealing with two straight lines.


 0 kommentar(er)
0 kommentar(er)
